by Ashis Pati
In the context of deep generative models, improving controllability by enabling selective manipulation of data attributes has been an active area of research. Latent representation-based models such as Variational Auto-Encoders (VAEs) have shown promise in this direction as they are able to encode certain hidden attributes of the data.
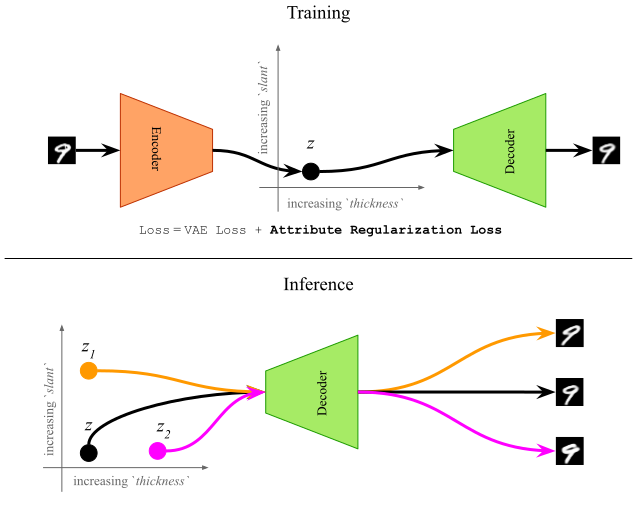
In this research work, we propose a supervised training method which uses a novel regularization loss to create structured latent spaces where specific continuous-valued attributes are forced to be encoded along specific dimensions of the latent space. For instance, if the attributes represents ‘thickness’ of a digit, and the regularized dimensions correspond to the first dimension of the latent space, then sampling latent vectors with increasing values of the first dimension should result in the same digit with increased thickness. This overall idea is shown in Figure 1 below. The resulting Attribute-Regularized VAE (AR-VAE) can then be used to manipulate these attributes by simple traversals along the regularized dimension.
AR-VAE has several advantages over previous methods. Unlike Fader Networks it is designed to work with continuous-valued attributes, and unlike GLSR-VAE, it is agnostic to the way attributes are computed or obtained.
Method
In order to create a structured latent space where an attribute $a$ is encoded along a dimension $r$, we add a novel attribute regularization loss to the standard VAE-objective. This loss is designed such that as we traverse along $r$, the attribute value $a$ of the generated data increases. To formulate the loss function, we consider a mini-batch of $m$ examples, and follow a three-step process:
1. Compute an attribute distance matrix $D_a$
2. Compute a regularized dimension distance matrix $D_r$
3. Compute the mean absolute error between signs of $D_a$ and $D_r$
In practice, we compute the hyperbolic tangent of $D_r$ so as to ensure differentiability of the loss function with respect to the latent vectors. Multiple regularization terms can be used to encode multiple attributes simultaneously. For a more detailed mathematical description of the loss function, check out the full paper.
Experimental Results
We evaluated AR-VAE using different datasets from the image and music domains. Here, we present some of the results of manipulating different attributes. For detailed results on other experiments such as latent space disentanglement, reconstruction fidelity, content preservation, and hyperparameter tuning, check out the full paper.
Manipulation of Image Attributes
Manipulating attributes of 2-d shapes. Each row in the figure below represents a unique shape (from top to bottom): square, heart, ellipse. Each column corresponds to traversal along a regularized dimension which encodes a specific attribute (from left to right): Shape, Scale, Orientation, x-position, y-position.
Manipulating attributes of MNIST digits. Each row in the figure below represents a unique digit from 0 to 9. Each column corresponds to traversal along a regularized dimension which encodes a specific attribute (from left to right): Area, Length, Thickness, Slant, Width, Height.
Manipulation of Musical Attributes
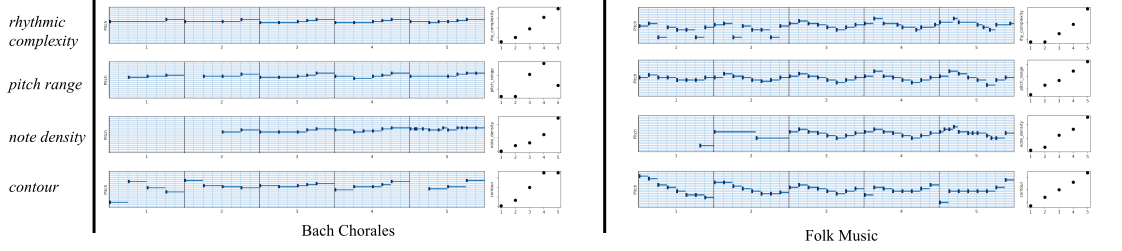
Manipulating attributes of monophonic measures of music. In the figure below, measures on each staff line are generated by traversal along a regularized dimension which encodes a specific musical attribute (shown on the extreme left).

Piano-roll version of the figure above is shown below. Plots on the right of each piano-roll show the progression of attribute values.
Conclusion
Overall, AR-VAE creates meaningful attribute-based interpolations while preserving the content of the original data. In the context of music, it can be used to build interactive tools or plugins to aid composers and music creators. For instance, composers would be able to manipulate different attributes (such as rhythmic complexity) of the composed music to try different ideas and meet specific compositional requirements. This would allow fast iteration and would be especially useful for novices and hobbyists. Since the method is agnostic to how the attributes are computed, it can potentially be useful to manipulate high-level musical attributes such as tension and emotion. This will be particularly useful for music generation in the context of video games where the background music can be suitably changed to match the emotional context of the game and the actions of the players.