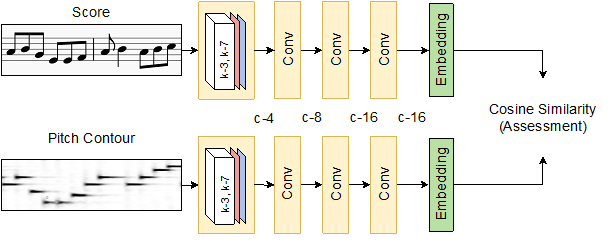
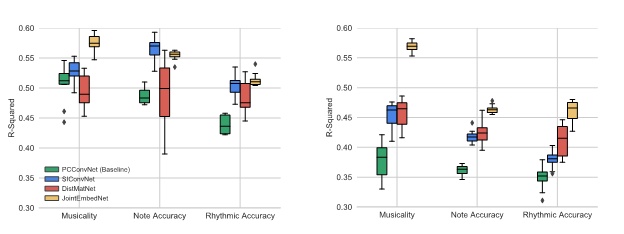
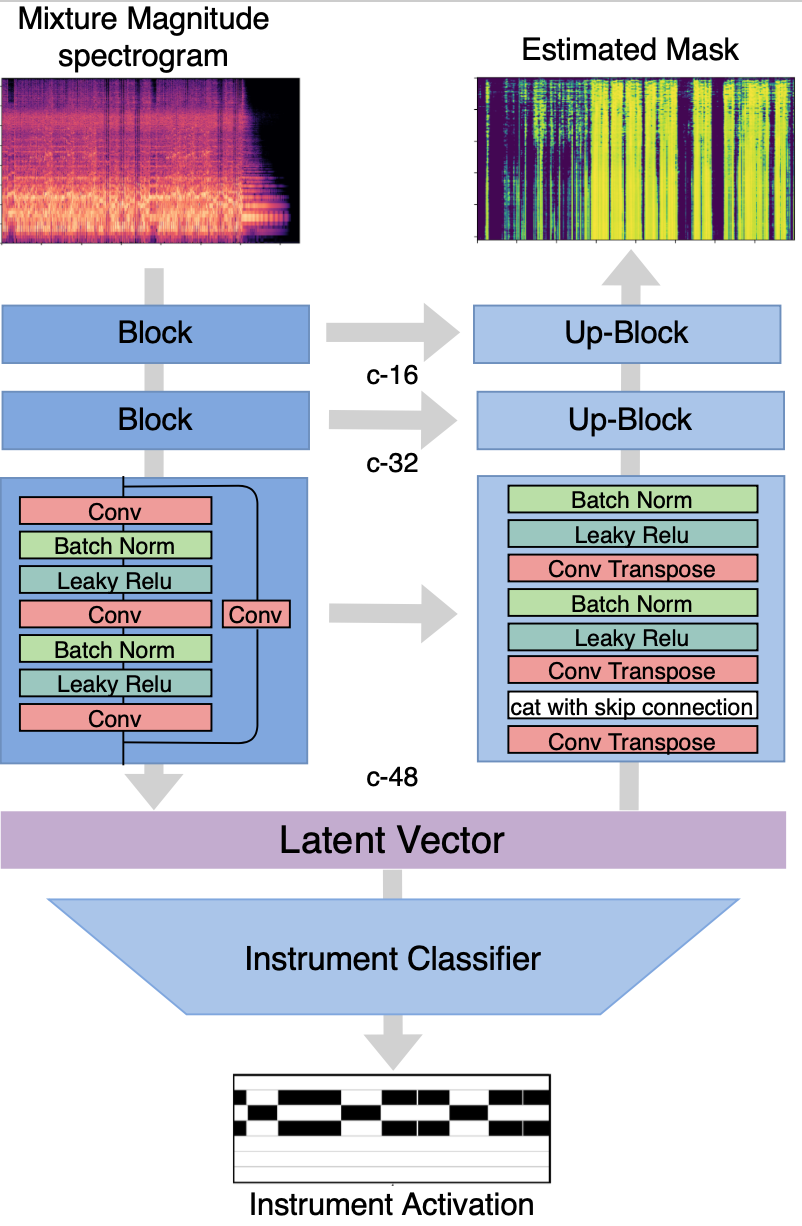
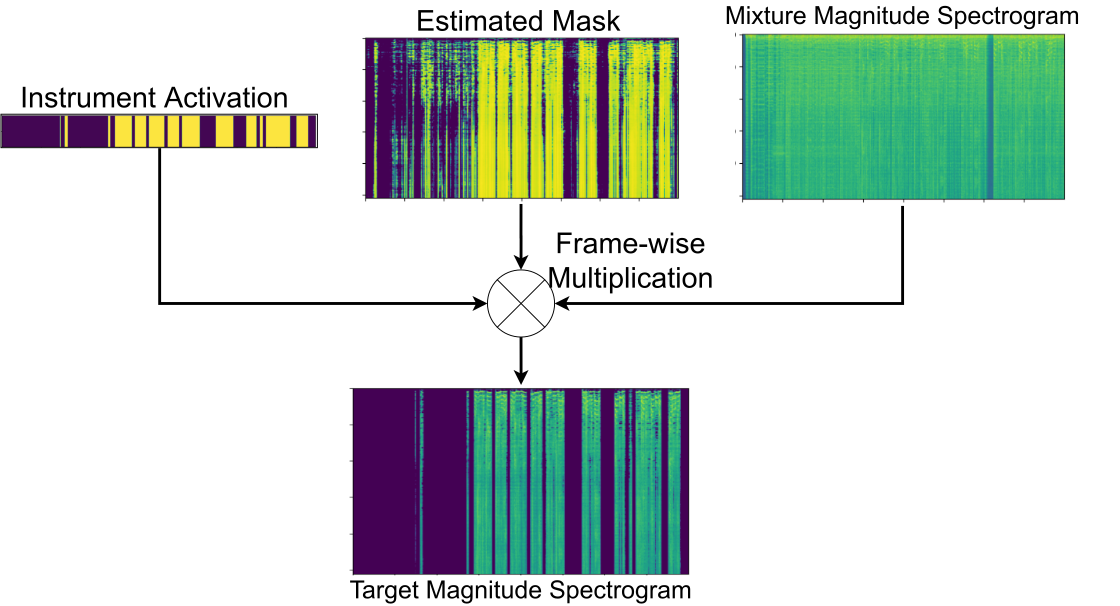
by Yiwei Ding
Due to the increasing use of neural networks, the last decade has seen dramatic improvements in a wide range of music classification tasks. However, the increased algorithmic complexity of the models requires an increased amount of data during the training process. Therefore, transfer learning is applied where the model is first pre-trained on a large-scale dataset for the source tasks and then fine-tuned with a comparably small dataset of the target task. T However, the increasing model complexity also makes the inference computationally expensive, so knowledge distillation is proposed where a low-complexity (student) model is trained while leveraging the knowledge in the high-complexity (teacher) model.
In this study, we integrate ideas and approaches from both transfer learning and knowledge distillation and apply them to the training of low-complexity networks to show the effectiveness of knowledge transfer for music classification tasks. More specifically, we utilize pre-trained audio embeddings as teachers to regularize the feature space of low-complexity student networks during the training process.
Methods
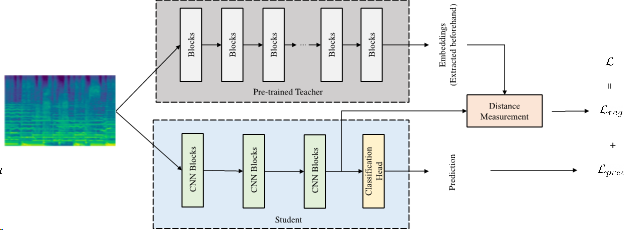
Similar to knowledge distillation, we rewrite our loss function as a combination of cross entropy loss for the classification task and a regularization loss that measures the distance between the student network’s feature map and the pre-trained embeddings with two different distance measures.
Experiments
We test the effectiveness of using pre-trained embeddings as teachers on two tasks: musical instrument classification with OpenMIC and music auto-tagging with MagnaTagATune, and we use four different embeddings: VGGish, OpenL3, PaSST and PANNs.
The following systems are evaluated for comparison:
• Baseline: CP ResNet (on OpenMIC) and Mobile FCN (on MagnaTagATune) trained without any extra regularization loss.
• TeacherLR: logistic regression on the pre-trained embeddings (averaged along the time axis), which can be seen as one way to do transfer learning by freezing the whole model except for the classification head.
• KD: classical knowledge distillation where the soft targets are generated by the logistic regression.
• EAsTCos-Diff: feature space regularization that uses cosine distance difference and regularizes only the final feature map.
• EAsTFinal and EAsTAll: proposed systems based on distance correlation as the distance measure, either regularizing only at the final stage or at all stages, respectively.
• EAsTKD: a combination of classical knowledge distillation and our method of using embeddings to regularize the feature space. The feature space regularization is done only at the final stage.
Results
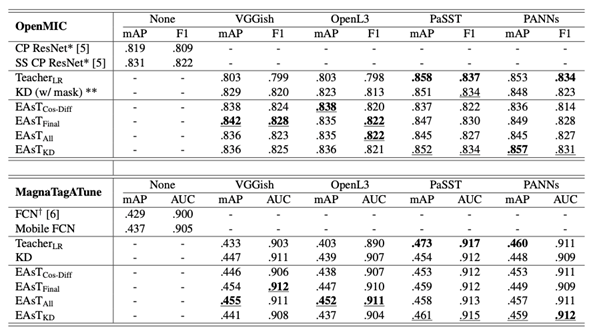
Table 1 shows the results on the OpenMIC and the MagnaTagATune dataset. We can make the following observations:
• Models trained with the extra regularization loss consistently outperform the non-regularized ones on both datasets, with all features and all regularization methods.
• Whether the teachers themselves have an excellent performance (PaSST and PANNs) or not (VGGish and OpenL3), students benefit from learning the additional knowledge from these embeddings, and the students’ upper limit is not bounded by the performance of teachers.
• As for the traditional knowledge distillation, the models perform best only with a “strong” teacher like PaSST and PANNs, which means the method is dependent on high-quality soft targets generated by the “strong” teachers.
• The combination system EAsTKD gives us better results with PaSST and PANNs embeddings while for VGGish and OpenL3 embeddings, the performance is not as good as EAsTFinal or EAsTAll in most cases.
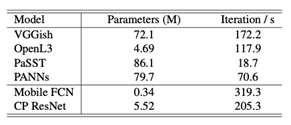
Table 2 lists the number of parameters as well as rough inference speed measurements of the models. We can see that Mobile FCN and CP ResNet are much faster in inference than pre-trained models.
Conclusion
In this study, we explored the use of audio embeddings as teachers to regularize the feature space of low-complexity student networks during training. We investigated several different ways of implementing the regularization and tested its effectiveness on the OpenMIC and MagnaTagATune datasets. Results show that using embeddings as teachers enhances the performance of the low-complexity student models, and the results can be further improved by com bining our method with a traditional knowledge distillation approach.
Resources
• Code: The code for reproducing experiments is available in our Github repository.
• Paper: Please see the full paper for more details on our study.