Inpainting as a Creative Tool
Inpainting is the task of automatically filling in missing information in a piece of media (say, an image or a audio clip). Traditionally inpainting algorithms have been used mostly for restorative purposes. However, in many cases, there could be multiple ways to perform an inpainting task. Hence, inpainting algorithms can be used as a creative tool.

Specifically for music, an inpainting model could be used for several applications in the field of interactive music creation such as:
- to generate musical ideas in different styles,
- to connect different musical sections, and
- to modify and extend solos.
Motivation
Previous work, e.g., Roberts et al.’s MusicVAE, has shown that Variational Auto-Encoder (VAE)-based music generation models show interesting properties such as interpolation and attribute arithmetic (this article gives an excellent overview of these properties). Effectively, for music, we can train a low-dimensional latent space where each point maps to a measure of music (see Fig. 3 for an illustration).

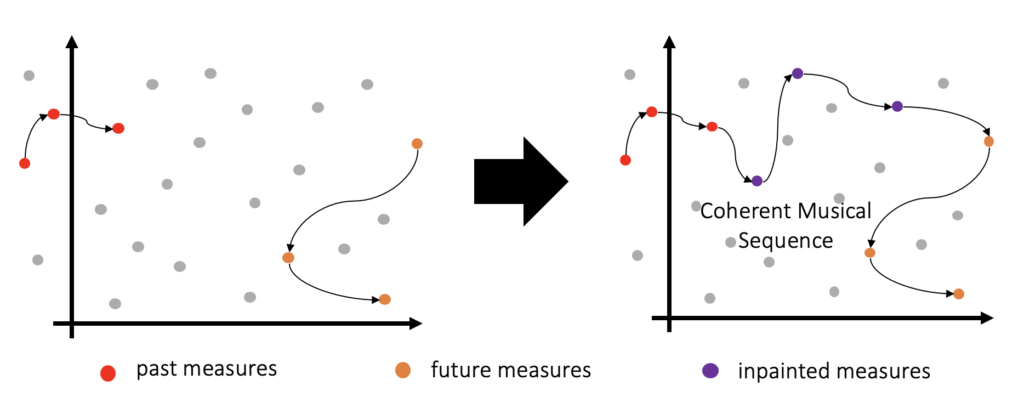
Now while linear interpolation in latent spaces has shown interesting results, by definition, it cannot model repetition in music (joining two points in euclidean space with a line will never contain the same point twice). The key motivation behind this research work was to explore if we can learn to traverse complex trajectories in the latent space to perform music inpainting, i.e., given a sequence of points corresponding to the measures in the past and future musical contexts, can we find a path through this latent space which can form a coherent musical sequence (see Fig. 4).
Method
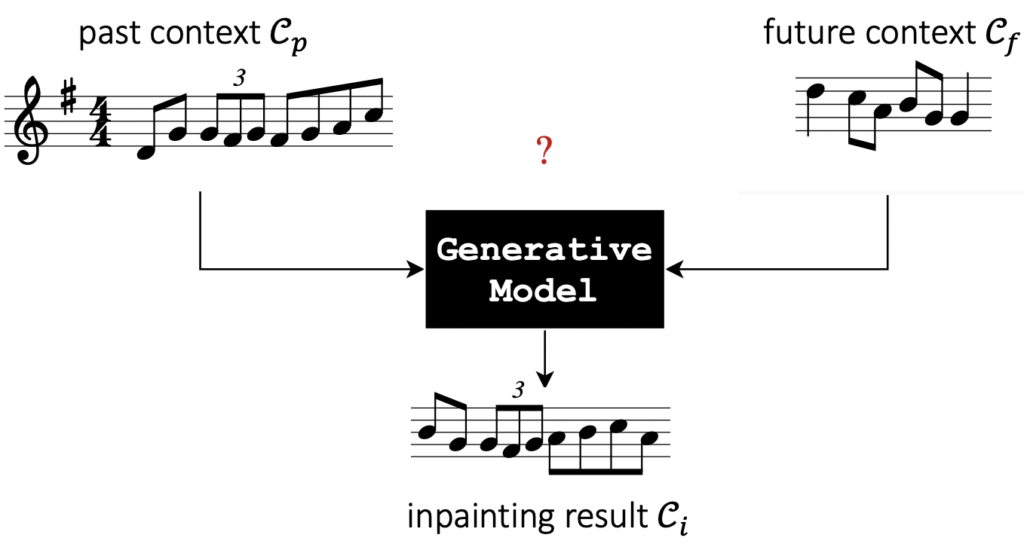
To formalize the problem, consider a situation where we are given the beginning and end of a song (which we refer to as the past musical context Cp and future musical context Cf, respectively) The task here is to create a generative model which connects the two contexts in a musically coherent manner by generating an inpainting Ci. We further constrain the task by assuming that the contexts and the inpainting have a certain number of measures (see Fig. 2 for an illustration). So effectively, we want to train a generative model which can maximize the likelihood of p(Ci|Cp, Cf).
In order to achieve the above objective, we train recurrent neural networks to learn to traverse the latent space. This is accomplished using the following steps:
-
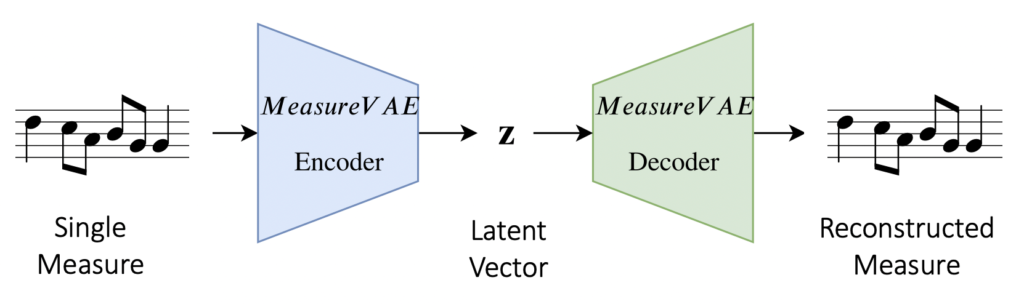
- We first train a MeasureVAE model to reconstruct single measures of music. This creates our latent space for individual measures.
-
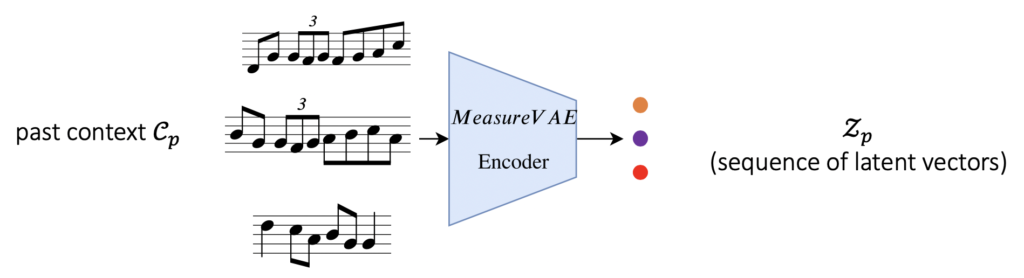
- The encoder of this model is used to obtain the sequence of latent vectors (Zp and Zf) corresponding to the past and future musical contexts.
-
- Next, we train a LatentRNN model which takes these latent vector sequences as input and learns to output another sequence of latent vectors Zi corresponding
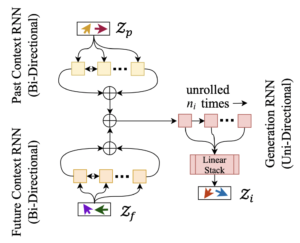
Figure 7: to the inpainted measures.
- Finally we use the decoder of the MeasureVAE to maps these latent vectors back to the music space to obtain our inpainting (Ci).
- Next, we train a LatentRNN model which takes these latent vector sequences as input and learns to output another sequence of latent vectors Zi corresponding
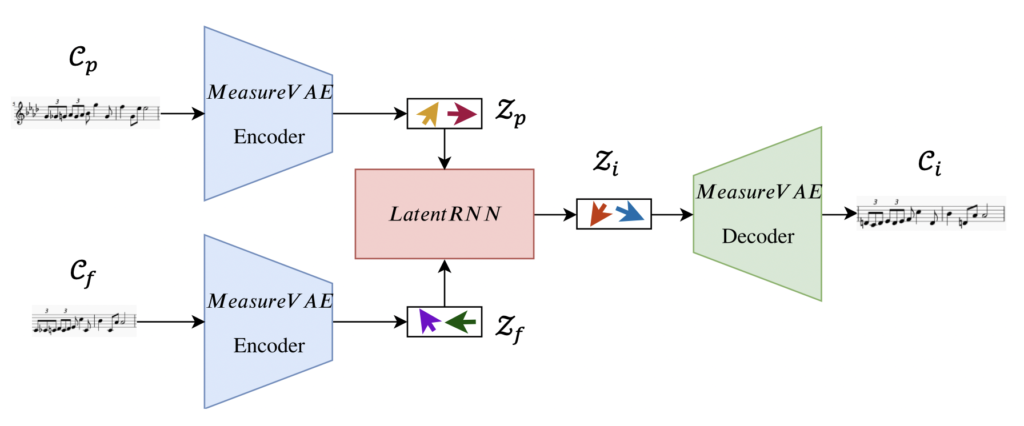
More details regarding the model architectures and the training procedures are provided in our paper and our GitHub repository.
Results
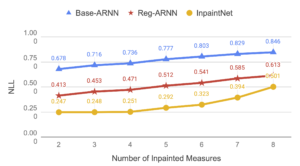
We trained and tested our proposed model on monophonic melodies in the Scottish and Irish style. For comparison, we used the AnticipationRNN model proposed by Hadjeres et al. and a variant of it based our stochastic training procedure. Our model was able to beat both the baselines in objective test aimed at testing how well the model is able to reconstruct missing measures in monophonic melodies.
We also conducted a subjective listening by asking human listeners to rate pairs of melodic sequences. In this our proposed model performed comparably to the baselines.
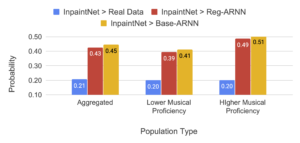
While the method works fairly well, there were certain instances where the model produces pitches which are out of key. We think these “bad” pitch predictions were instrumental in reducing the perceptual rating of the inpaintings in the subjective listening test. This needs additional investigation. Interested readers can listen to some of these example inpaintings performed by our model in the audio examples list.
Overall, the method demonstrates the merit of learning complex trajectories in the latent spaces of deep generative models. Future avenues of research would include adapting this framework for polyphonic and multi-instrumental music.
Resources
- Full paper
- Conference short presentation video
- GitHub repository
- Audio examples